La factorización
La factorización es el proceso algebraico por medio del cual se transforma una suma o resta de términos algebraicos en un producto algebraico.
También se puede entender como el proceso inverso del desarrollo de productos notables.
Factor común
Reglas para obtener el factor común de un polinomio
- Se obtiene el máximo común divisor de los coeficientes
- Se identifica las literales con menor exponente que se repitan en cada uno de los términos algebraicos del polinomio a factorizar.

Ejemplos de factorización de un polinomio con factor común:
- 1.- En la expresión
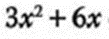
El máximo común divisor de los coeficientes (3 y 6) es 3.
Y la literal que repite con menor exponente es x.
Por lo tanto, el factor común es 3x
Después cada uno de los elementos del polinomio se divide por el factor común:
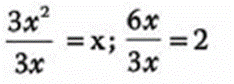
y el resultado de la factorización es:
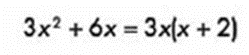
Factorización por agrupación
En la factorización por agrupación, no todos los elementos del polinomio comparten un factor común, por lo que se deben identificar primero los grupos de elementos que si comparten términos comunes y después factorizar cada grupo de elementos.

Ejemplos:
- 1.- Factorizar:
.
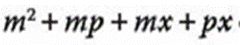
Agrupamos:
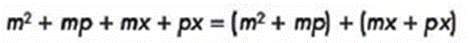
Y factorizamos los grupos:
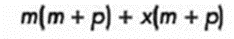
Diferencia de cuadrados (x2 – y2)
La diferencia de cuadrados tiene la forma de x2 – y2 y su factorización es el producto de binomios conjugados:

Ejemplos:
- 1.- Factorizar:
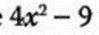
Primero obtenemos la raíz de cada elemento del binomio:

Y factorizamos:
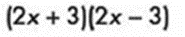
Trinomio al cuadrado perfecto (x2 + 2xy + y2)
Resultado:
Es un binomio al cuadrado

Reglas para factorizar un trinomio al cuadrado perfecto
- Se ordenan los términos del trinomio en orden descendente a una de las literales, de forma que los extremos sean expresiones que tengan raíz cuadrada exacta
- Se obtiene la raíz del primer y tercer termino
- Para comprobar que haya sido un trinomio al cuadrado “perfecto”, se realiza el doble producto de los términos obtenidos en el paso dos y debe ser igual al 2do término del trinomio.
- El signo del binomio que dio resultado es el mismo que el signo del 2do término del trinomio original
Ejemplos:
- 1.- Factorizar:
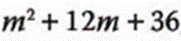
Obtenemos las raíces:

Se comprueba multiplicando el doble de las raíces:
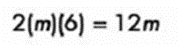
Se agrupan las raíces y el signo coincide con el termino central del trinomio:
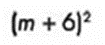
Trinomio de la forma: (x2 + bx + c)
Resultado:
Producto de dos binomios con término común: (x+e)(x+h)

Reglas para factorizar un trinomio de la forma (x2 + bx + c):
- Se ordenan los términos del trinomio en orden descendente a una de las literales, de forma que el primer término sea una expresión que tenga raíz cuadrada exacta
- Se obtiene la raíz cuadrada de este primer término y se coloca en los dos binomios
- Se buscan dos números que su producto sea igual al 3er término del trinomio (c) y su suma aritmética sea igual al coeficiente del 2do término del trinomio (b). De estos números, el mayor se coloca en el primer binomio y el menor en el segundo binomio.
- x2 + (e + h) x + (e * h) = (x + e) (x + h)
- El signo del primer binomio es igual al signo del 2do término del trinomio, y el signo del segundo binomio es igual al signo resultante del producto de los signos del 2do por el 3er término del trinomio.

Ejemplos:
- 1.- El desarrollo del trinomio:
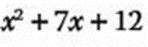
Se obtienen la raíz cuadrada del primer término para colocarlo en los dos binomios:
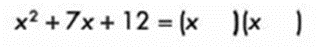
Se colocan los signos según la regla del punto 4
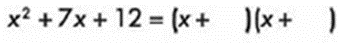
Se buscan los coeficientes según la regla del punto 3
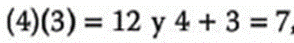
El resultado es:
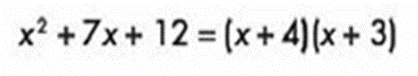
Trinomio de la forma (ax2 + bx + c)
Resultado:
Producto de dos binomios: (fx + e)(x + h)

Reglas para factorizar un trinomio de la forma (ax2 + bx + c):
- Se ordenan los términos del trinomio en orden descendente a una de las literales
- Se multiplica y se divide el trinomio por el coeficiente del 1er termino
- Con esto, el trinomio del numerador se factoriza a dos binomios con termino común
- A cada uno de estos dos binomios se les divide por el denominador para obtener los dos binomios de la forma: (fx + e) (x + h)
Ejemplos:
- 1.- Factorizar
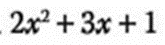
Se multiplica y se divide por el coeficiente del término cuadrático:
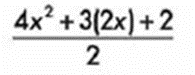
Se factoriza el numerador en dos binomios con termino común y se divide a cada uno de ellos por el denominador:
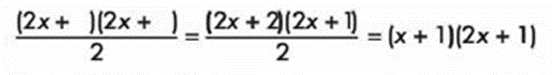
Suma y diferencia de cubos: (x3 ± y3)
Resultado:
Producto de un binomio por un trinomio

Reglas para factorizar una suma o diferencia de cubos:
- Se obtienen las raíces de cada uno de los términos
- El primer término es un binomio igual a la suma o resta de estas raíces obtenidas
- El segundo término es un trinomio igual:
1er termino: Igual al cuadrado de la raíz del primer término del binomio
2do término: Igual al producto de las raíces del binomio con signo opuesto.
3er término: Igual al cuadrado de la raíz del segundo término del binomio
Ejemplos:
- 1.- Factorizar:
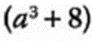
Se obtienen las raíces cubicas de cada uno de los términos:

Se desarrolla el trinomio y obtenemos:
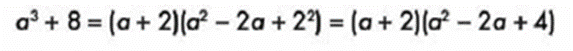
Mas ejercicios, problemas y preguntas de simulación en nuestra guía desarrollada para el ingreso al bachillerato (COMIPEMS y UNAM):
-
Producto en oferta
 Guía de Historia de México para el examen COMIPEMS-UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00.
Guía de Historia de México para el examen COMIPEMS-UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00. -
Producto en oferta


 Guía de Formación Cívica y Ética para examen COMIPEMS-UNAMEl precio original era: $70.00.$50.00El precio actual es: $50.00.
Guía de Formación Cívica y Ética para examen COMIPEMS-UNAMEl precio original era: $70.00.$50.00El precio actual es: $50.00. -
Producto en oferta


 Guía de Historia Universal para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00.
Guía de Historia Universal para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00. -
Producto en oferta


 Guía de Habilidad Verbal para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00.
Guía de Habilidad Verbal para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00. -
Producto en oferta


 Guía de Habilidad Matemática para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00.
Guía de Habilidad Matemática para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00. -
Producto en oferta


 Guía de Biología para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00.
Guía de Biología para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00. -
Producto en oferta


 Guía de Matemáticas para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00.
Guía de Matemáticas para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00. -
Producto en oferta


 Guía de Español para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00.
Guía de Español para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00.
-
Producto en oferta


 Guía de Historia Universal para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00.
Guía de Historia Universal para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00. -
Producto en oferta


 Guía de Habilidad Verbal para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00.
Guía de Habilidad Verbal para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00. -
Producto en oferta


 Guía de Habilidad Matemática para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00.
Guía de Habilidad Matemática para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00. -
Producto en oferta


 Guía de Biología para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00.
Guía de Biología para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00. -
Producto en oferta


 Guía de Matemáticas para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00.
Guía de Matemáticas para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00. -
Producto en oferta


 Guía de Español para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00.
Guía de Español para el examen COMIPEMS UNAM 2024El precio original era: $70.00.$50.00El precio actual es: $50.00.


