Ecuaciones de segundo grado: solución algebraica, gráfica y aplicación

Métodos para resolver ecuaciones de 2do grado:

La resolución de ecuaciones de segundo grado es el cálculo que se realiza para encontrar el valor aritmético de la variable (incógnita) que satisfaga la igualdad.

También se dice que se encuentran las “raíces” de la ecuación.

Los métodos para resolver las ecuaciones de segundo grado son:

• Por la formula general:

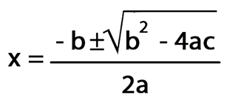
• Por factorización

• Completando trinomio cuadrado perfecto

Antes de resolver una ecuación podemos saber si la ecuación tiene alguna solución, aplicando unos discriminantes a sus coeficientes.

• 1.- Si b2 – 4ac = 0, la ecuación tiene solución

• 2.-Si b2 – 4ac < 0, las raíces son imaginarias

• 3.-Si b2 – 4ac > 0, las raíces son reales.

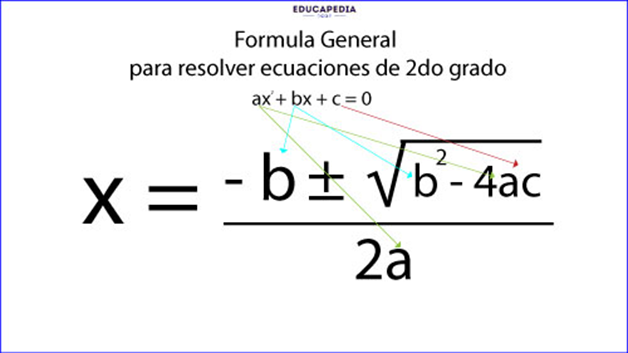
La fórmula general para resolver ecuaciones de 2do grado

Procedimiento:

1. Se sustituyen los coeficientes indicados
2. Se obtienen 2 valores, uno aplicando el signo positivo al radical y otro valor cuando se aplica el signo negativo al mismo radical.

OJO:

Si algún coeficiente no existe en la ecuación de segundo grado, quiere decir que su valor es igual a cero.

Ejemplos:

• 1.- Resolver la ecuación:

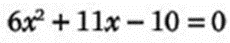
          Los valores a sustituir son:

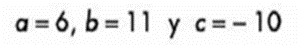
          Sustituyendo tenemos:

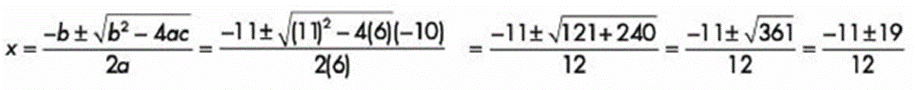
          Las raíces o soluciones son:

Segundo método para resolver ecuaciones de 2do grado: Por factorización y despeje

Procedimiento:

1. Se factoriza la ecuación a resolver
2. Cada factor se igual a cero
3. Se despeja el valor de la incógnita de cada factor

Ejemplo:

• 1.- Obtener las raíces de:

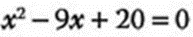
          Factorizamos:

          Igualamos a cero y despejamos la incógnita:

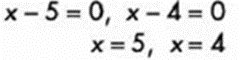
Tercer método para resolver ecuaciones de 2do grado: Completando el trinomio al cuadrado perfecto

Procedimiento:

1. Con la ecuación inicial trata de completar un trinomio al cuadrado perfecto
2. Para después factorizarlo en un binomio al cuadrado
3. Y por último despejar la variable y obtener su valor.

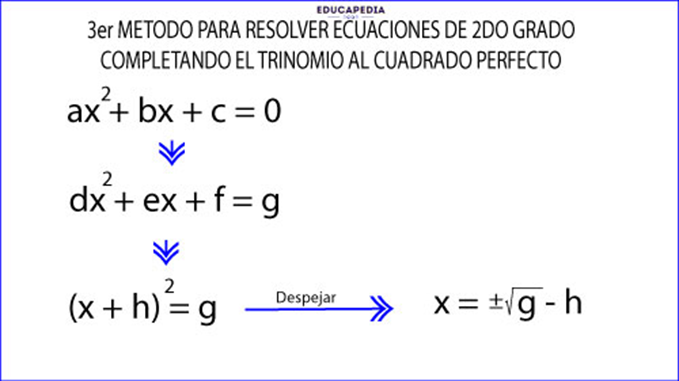
Ejemplos:

• 1.- Encontrar las raíces de:

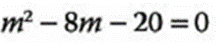
Se completa el trinomio al cuadrado perfecto:

Se forma el binomio al cuadrado:

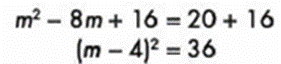
Se despeja la incógnita:

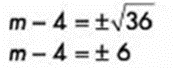
Mas ejercicios, problemas y preguntas de simulación en nuestra guía desarrollada para el ingreso al bachillerato (COMIPEMS y UNAM):