Un sistema de dos ecuaciones con dos incógnitas es de la forma:

Ax + By = C

A₁x + B₁y = C₁

Para las cuales existen un valor de “x” y un valor de “y” que resuelve la ecuación.

Donde:

         A, B, C, A₁, B₁ y C₁ son constantes llamados coeficientes.

         “x” y “y” son las variables del sistema con exponente igual a 1

Ejemplos:

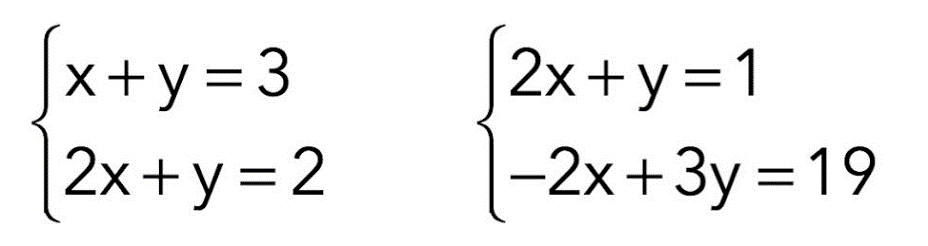
Métodos de solución

Para resolver un sistema de dos ecuaciones con dos incógnitas

Ax + By = C

A₁x + B₁y = C₁

Se pueden aplicar varios métodos. Sin embargo, antes de intentar resolverlas, podemos saber qué tipo de solución tiene el sistema.

Existen 3 tipos de soluciones:

1.-Una solución: Son los sistemas que solo tienen una solución, donde se tiene que encontrar el valor de “x” y de “y”.

2.-Una infinidad de soluciones: Si una ecuación del sistema se puede obtener por la multiplicación o división de un numero por la otra ecuación del sistema, entonces las dos ecuaciones son equivalentes.

3.-No tienen soluciones: Si A/A₁ = B/B₁ = k   y C/C₁ es diferente de k

REPRESENTACIÓN GEOMÉTRICA DE UN SISTEMA DE DOS ECUACIONES LINEALES

En términos geométricos, cada ecuación representa una línea en el plano cartesiano.

1.-Si son líneas diferentes, en algún punto se cruzan y ese punto representa la solución al sistema de 2 ecuaciones (x, y)

2.-Si son la misma línea, tendrán una infinidad de soluciones, ya que son ecuaciones semejantes

3.-Si son dos líneas diferentes pero paralelas, están no tendrán solución, ya que geométricamente no tienen un punto donde se intersecten.

Ejemplo

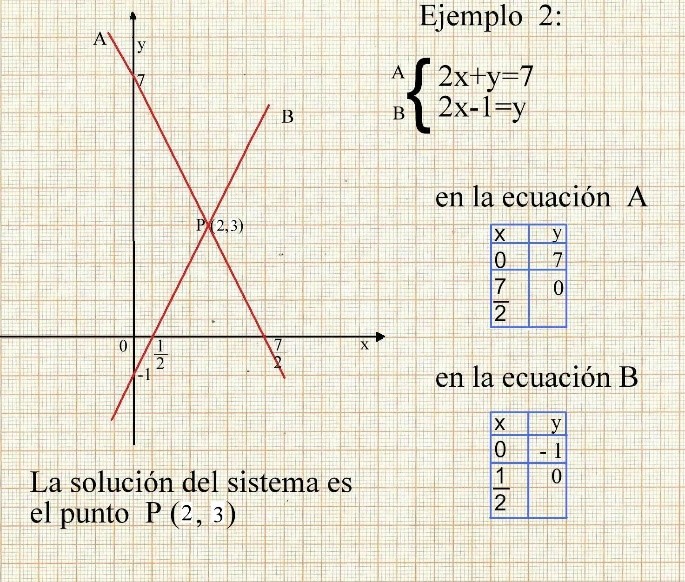
Después de haber conocido las posibilidades de solución y su representación geométrica, podemos utilizar alguno de los siguientes métodos para resolver el sistema.

MÉTODOS DE SOLUCIÓN:

         1.- Regla de Cramer o Método por determinantes

         2.- Método de Reducción o de suma y resta:

         3.- Método por sustitución:

Regla de Cramer o por determinantes:

Un determinante de 2 x 2 se representa como un arreglo de la siguiente forma:

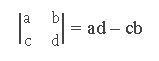
Dado un sistema de 2 ecuaciones:

Ax + By = C

A₁x + B₁y = C₁

Para resolver y obtener los valores de “x” y “y” aplicamos la siguiente regla:

El numerador determinante se obtiene sustituyendo los coeficientes de la variable a obtener por el coeficiente “c”

El denominador determinante se obtiene con los coeficientes de las variables “x” y “y”.

Método de Reducción o de suma y resta:

Este método consiste en:

1.- Eliminar una de las variables al sumar las dos ecuaciones y obtener una ecuación de primer grado con una variable

2.- Despejar esta variable y así obtener su valor.

3.- Se sustituye en cualquiera de las dos ecuaciones y se obtiene el valor de la otra variable.

Método por sustitución

En este método:

1.- Se elige una ecuación para despejar una de sus incógnitas

2.- Se sustituye en la otra ecuación, de esta manera se obtiene una ecuación de primer grado con una incógnita.

3.- En esta ecuación se despeja la incógnita y se obtiene su valor.

4.-Por ultimo este valor se sustituye en la otra ecuación y se obtiene el valor de la otra incógnita.