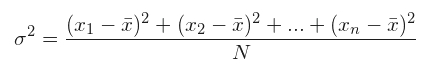MEDIDAS DE TENDENCIA CENTRAL
Las medidas de tendencia central son las medidas que nos indican cierto comportamiento general de un conjunto de datos.
Las medidas de tendencia central más conocidas son:
1.- La media aritmética o promedio
2.- La mediana
3.- La moda
4.- La media geométrica
5.- La media Armónica
1.- La media aritmética o promedio
La media aritmética o promedio es la suma de los valores del conjunto de datos que estamos considerando entre el número de datos que tenemos.
La fórmula es: 
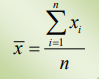
Ejemplo:
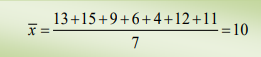
Para un conjunto de valores tenemos:
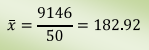
2.- La mediana
La mediana es el valor central de un conjunto ordenado de datos.
Por ejemplo:
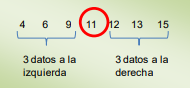
Si tenemos dos datos:
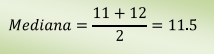
3.- La moda
La moda es el valor más frecuente en un conjunto de datos.
Un conjunto de datos puede no tener moda o tener más de 1.
Por ejemplo:
La moda de este conjunto de datos es: 15

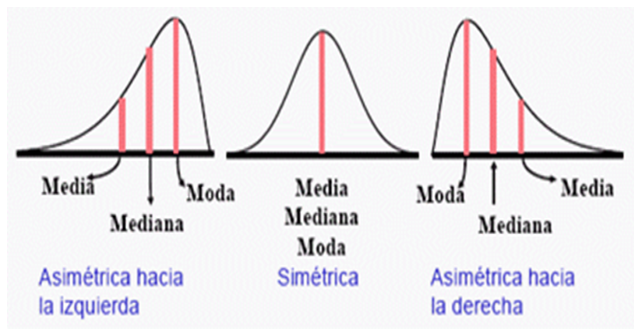
COMPARACIÓN GRÁFICA ENTRE MEDIA, MEDIANA Y MODA
4.- La media geométrica
La media geométrica de un conjunto de valores es la raíz n-ésima del producto de los valores de dicho conjunto.
Si hay dos valores, la raíz cuadrada del producto de estos dos; si son tres, es la raíz cúbica del producto de los tres valores.
La fórmula general es:
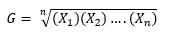
5.- La media Armónica
La media armónica de un conjunto de números es igual al recíproco, o inverso, de la media aritmética de los recíprocos de dichos valores.
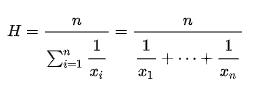
La media armónica resulta poco influida por la existencia de valores muy grandes, siendo en cambio más sensible a valores mucho más pequeños.
MEDIDAS DE DISPERSIÓN
Las medidas de dispersión son números o valores que nos indican que tanto los valores de un conjunto de datos “salen o se dispersan” de un comportamiento de agrupación (medidas de tendencia central).
Las medidas de dispersión más comunes son:
1.- El Rango
2.- La desviación estándar
3.- La varianza
1.- El Rango
El rango de un conjunto de números es la diferencia entre el mayor y el menor de todos ellos.
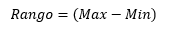
2.- La desviación estándar
La desviación típica o desviación estándar es la medida que nos indica que tanto se agrupan los datos de su media o que tanto se dispersan.
También se puede decir que es la raíz cuadrada de su varianza.
La fórmula es:
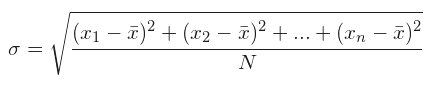
3.- La varianza
La varianza es la media aritmética de los cuadrados de las desviaciones respecto a la media aritmética, es decir, es el promedio de las desviaciones de la media elevadas al cuadrado.