LOGARITMO

El logaritmo de un número (argumento), es igual a otro número(logaritmo), de tal forma que este último número que estamos buscando, sirve como exponente de una base y dé como resultado el primer número (argumento).

Por ejemplo, el logaritmo decimal (base 10) de 100 es 2, porque 10² = 100

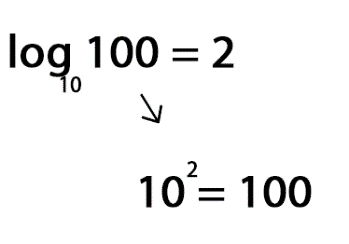
PROPIEDADES DE LOS LOGARITMOS

1.- El logaritmo de un producto es igual a la suma de los logaritmos de los factores.

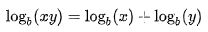
2.- El logaritmo de un cociente es igual al logaritmo del numerador menos el logaritmo del denominador.

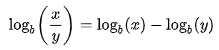
3.-El logaritmo de una potencia es igual al producto entre el exponente y el logaritmo de la base de la potencia.

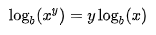
4.- El logaritmo de una raíz es igual al producto entre la inversa del índice y el logaritmo del radicando.

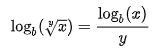
Las bases más utilizadas en los logaritmos son 10 y e (Número de Euler, e = 2,718281828459…)

Cuando usamos la base 10, no es necesario escribir la base:

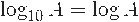
Al logaritmo con base “e” se le conoce como logaritmo neperiano (o logaritmo natural) y se representa así:

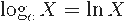
OPERACIONES CON EXPONENTES

Las operaciones con exponentes se derivan de la actividad matemática llamada potenciación.

Donde un número “a” (llamado base) se eleva a otro número “b” (llamado exponente).

E indica que la base “a” se debe multiplicar por si misma el número de veces que indique el exponente “b”.

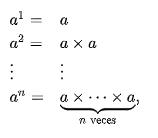
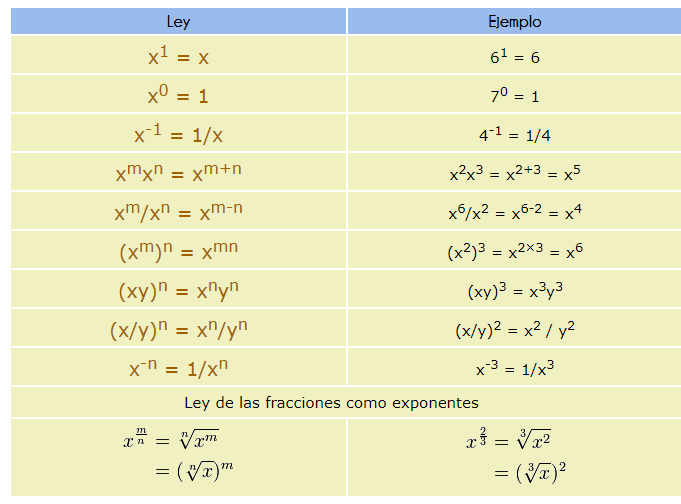
LEYES DE LOS EXPONENTES