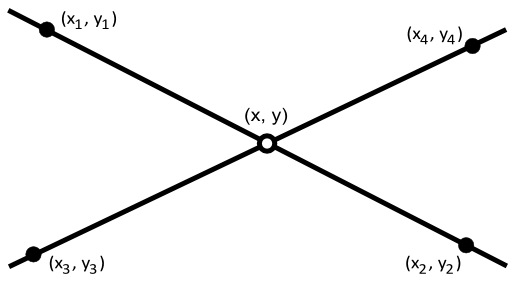
La intersección de rectas es cuando dos líneas rectas o más coinciden o “se tocan en un punto”.
En general, dos líneas rectas en un plano pueden tener 3 resultados diferentes:
1.-Se tocan en un solo punto
2.-No se tocan en ningún punto, son paralelas
3.-Se tocan en todos los puntos, son líneas idénticas
Intersección de dos rectas
Para encontrar el punto donde dos líneas de cortan:
1.-Se igualan las ecuaciones de las líneas
2.-Se resuelve la ecuación resultante
3.-El resultado es el punto donde se cortan
Ojo: si no tiene solución la ecuación resultante, es que las líneas no se cortan.
Intersección de líneas rectas en un triangulo
Mediana: Es el segmento de recta que une un vértice del triángulo con el punto medio del lado opuesto.
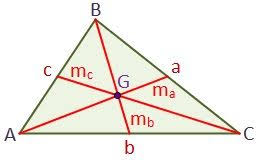
Para obtener la ecuación de la mediana:
1-Se utiliza la ecuación de la recta que pasa por 2 puntos
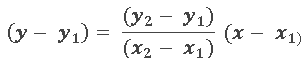
2.-En esta ecuación se sustituye (x1, y1) por el vértice desde donde se vaya a tomar la mediana.
3.-Para obtener el otro punto (x2, y2) se obtiene a partir de la fórmula para el punto medio de una recta.

En este caso, (x1, y1), (x2, y2) serán los valores del lado opuesto al vértice donde salga la mediana
Mediatriz: Es la recta que pasa por el punto medio de un lado de un triángulo y que es perpendicular a ese mismo lado.
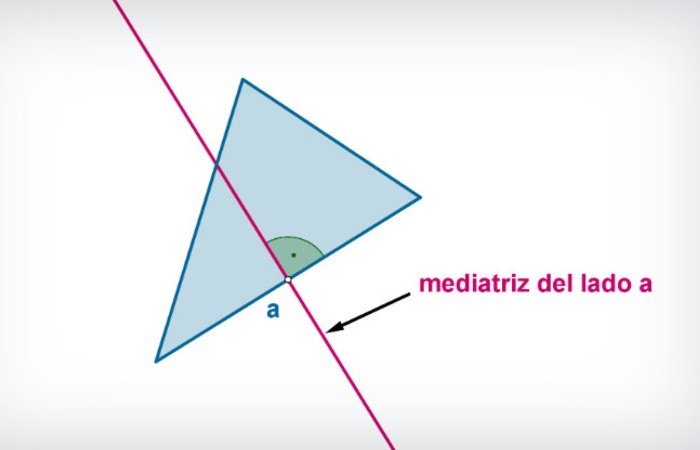
Para obtener la ecuación de la mediatriz de un triángulo:
1-Se utiliza la ecuación de la recta punto-pendiente
y – y1 = m (x – x1)
2.-En esta ecuación se sustituye (x1, y1) por el punto medio del lado donde se vaya a tomar la mediatriz, ocupando las fórmulas para el punto medio:

3.-Para obtener la pendiente m, se calcula la pendiente de este mismo lado y se aplica la perpendicularidad de las líneas.
m1 = – (1/ m2) o m1 + m2 = -1
Altura: Es el segmento de recta perpendicular trazado desde un vértice del triángulo hacia el lado opuesto.
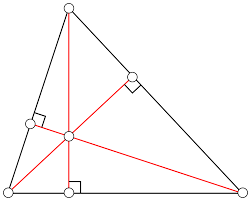
Para obtener la ecuación de la altura de un triángulo:
1-Se utiliza la ecuación de la recta punto-pendiente
y – y1 = m (x – x1)
2.-En esta ecuación se sustituye (x1, y1) por el vértice desde donde se vaya a tomar la altura.
3.-Para obtener la pendiente m, se calcula la pendiente del lado opuesto al vértice anterior y se aplica la perpendicularidad de las líneas.
m1 = – (1/ m2) o m1 + m2 = -1
PUNTOS DE INTERSECCIÓN EN UN TRIANGULO:
BARICENTRO:
Es el punto donde se intersectan las medianas
Para obtener sus coordenadas, utilizamos la formula siguiente:
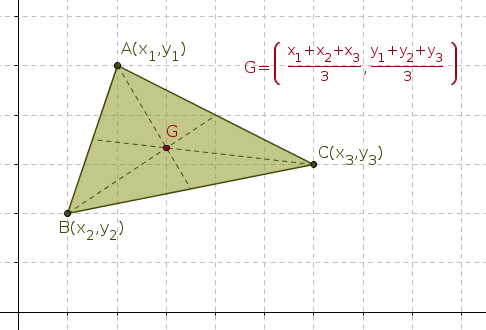
CIRCUNCENTRO:
Es el punto donde se intersectan las mediatrices.
También se llama circuncentro, porque si trazamos un circulo que toque los vértices del triángulo en cuestión, el circuncentro, será el centro del circulo trazado.
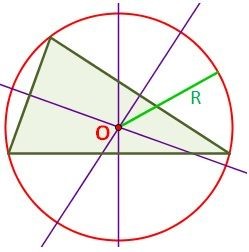
Para hallar las coordenadas del circuncentro:
1.-Se deben obtener las ecuaciones de dos de las mediatrices
2.-Con esto se resuelve el sistema de dos ecuaciones con 2 incógnitas para obtener el punto en el que se intersectan, el cual será el circuncentro del triangulo
ORTOCENTRO:
Es el punto donde se intersectan las alturas
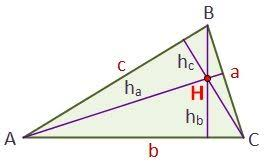
Para hallar las coordenadas del ortocentro:
1.-Se deben obtener las ecuaciones de dos de las alturas
2.-Con esto se resuelve el sistema de dos ecuaciones con 2 incógnitas para obtener el punto en el que se intersectan, el cual será el ortocentro del triangulo