Tema especial para el examen de la Universidad de Guadalajara (UdeG) 2025
Ecuaciones de segundo grado (cuadráticas)

Las ecuaciones de segundo grado (también llamadas cuadráticas) son aquellas donde el exponente de alguna de sus literales (incógnitas) es igual a 2 (elevada al cuadrado).
Tipos de ecuaciones de 2do grado
- Con 1 variable
- Con 2 o más variables
Ojo:
“Regularmente las que se estudian son con 1 variable”
Ecuaciones cuadráticas con 1 variable
Las ecuaciones de 2do grado tienen la forma ax2 + bx + c = 0
donde:
a, b y c son constantes y numero reales y “a” es diferente de cero.
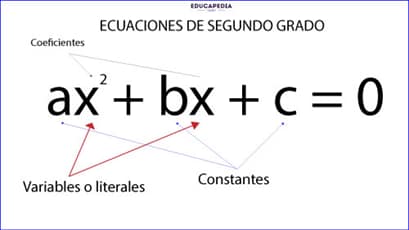
Ejemplos:
En la ecuación

se tiene a = 2, b = −3, c = 1
Resolución de ecuaciones de segundo grado
La resolución de ecuaciones de segundo grado es el cálculo que se realiza para encontrar el valor aritmético de la variable (incógnita) que satisfaga la igualdad.
También se dice que se encuentran las “raíces” de la ecuación.
Los métodos para resolver las ecuaciones de segundo grado son:
- Por la formula general:
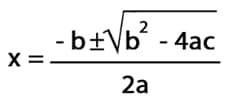
- Por factorización
- Completando trinomio cuadrado perfecto
Discriminante
Antes de resolver una ecuación podemos saber si la ecuación tiene alguna solución, aplicando unos discriminantes a sus coeficientes.
- 1.- Si b2 – 4ac = 0, la ecuación SI tiene solución
- 2.-Si b2 – 4ac < 0, No tiene soluciones reales, (las raíces son imaginarias)
- 3.-Si b2 – 4ac > 0, la ecuación SI tiene solución, (las raíces son reales)
La fórmula general para resolver ecuaciones de 2do grado
Procedimiento:
- Se sustituyen los coeficientes indicados
- Se obtienen 2 valores, uno aplicando el signo positivo al radical y otro valor cuando se aplica el signo negativo al mismo radical.

Ojo: Si algún coeficiente no existe en la ecuación de segundo grado, quiere decir que su valor es igual a cero.
Ejemplos:
- 1.- Resolver la ecuación:

Los valores a sustituir son:

Sustituyendo tenemos:
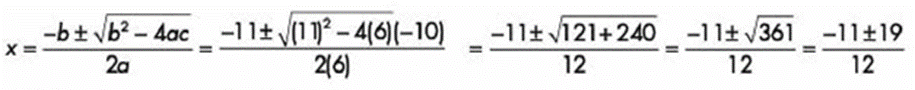
Las raíces o soluciones son:

Segundo método para resolver ecuaciones de 2do grado: Por factorización y despeje
Procedimiento:
- Se factoriza la ecuación a resolver
- Cada factor se igual a cero
- Se despeja el valor de la incógnita de cada factor

Ejemplo:
- 1.- Obtener las raíces de:

Factorizamos:

Igualamos a cero y despejamos la incógnita:

Ecuaciones racionales
Una ecuación racional es aquella en la que la variable aparece en el denominador de una fracción.
Resolver este tipo de ecuaciones requiere aplicar conceptos de fracciones algebraicas, mínimo común múltiplo (MCM) y simplificación.
Definición forma de ecuación racional
Una ecuación racional es una igualdad que contiene al menos una expresión racional, es decir, una fracción algebraica:


Ejemplo:

Restricciones del dominio
Antes de resolver, se deben determinar los valores prohibidos: aquellos que hacen que el denominador sea cero.
Ejemplo:
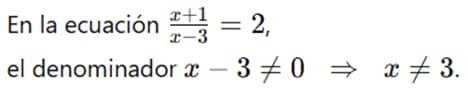
Pasos para resolver ecuaciones racionales
- Identificar los denominadores y establecer las restricciones (valores prohibidos).
- Encontrar el mínimo común denominador (MCD o MCM) de las fracciones.
- Multiplicar toda la ecuación por el MCM para eliminar los denominadores.
- Resolver la ecuación resultante (que será polinómica o más simple).
- Verificar las soluciones, descartando aquellas que sean valores prohibidos.
Ejemplo:
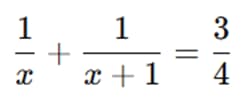
Solución:
- Restricciones: 𝑥 ≠ 0, 𝑥 ≠ −1
- MCM: 4x(x+1).
- Multiplicamos toda la ecuación por 4x(x+1):

Simplificamos:

Factorizamos:
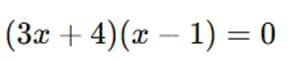
Soluciones: x = −4/3, x = 1.
Tipos de ecuaciones racionales
Sencillas: solo tienen una fracción con variable en el denominador.

Con varios denominadores: requieren MCM para unificarlos.

Con expresiones cuadráticas en el denominador: pueden dar lugar a ecuaciones de segundo grado.

Ecuaciones con radicales
Una ecuación con radicales es aquella en la que la incógnita aparece dentro de un signo de raíz.
Resolver este tipo de ecuaciones implica eliminar los radicales y obtener una ecuación equivalente (lineal, cuadrática o de mayor grado)
Definición formal de ecuación con radical:
Una ecuación con radicales es una igualdad de la forma:

donde:
- f(x) y g(x) son expresiones algebraicas,
- n es el índice del radical,
- y la incógnita x aparece dentro de la raíz.
Ejemplos:

Pasos para resolver ecuaciones con radicales
- Aislar el radical (si es posible).
- Elevar ambos lados de la ecuación a la potencia correspondiente para eliminar el radical.
- Si es raíz cuadrada → elevar al cuadrado.
- Si es raíz cúbica → elevar al cubo.
- Etc.
- Resolver la ecuación resultante.
- Verificar las soluciones sustituyendo en la ecuación original (para descartar soluciones extraviadas).
Ejemplos
Ejemplo 1: Raíz cuadrada
Elevamos al cuadrado:
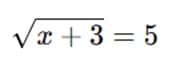

Restamos 3:
x = 22

Ejemplo 2: Radical con binomio

Restricción:
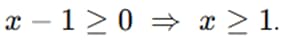
Elevamos al cuadrado:

Pasamos todo a un lado:
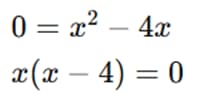
Soluciones candidatas: x = 0, x = 4.
Verificación:

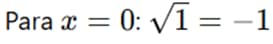
No es valida
Solución: x = 4
Próximo tema según la guía oficial para el examen de la Universidad de Guadalajara (UdeG) 2025:
Aquí puedes ver las guías de estudio desarrolladas para prepararte para el examen de la Universidad de Guadalajara (UdeG):
Guía de matemáticas para el examen de la Universidad de Guadalajara
Prepárate con esta guía desarrollada de matemáticas para el examen de la Universidad de Guadalajara 2025.
- Todos los temas desarrollados con ejercicios y preguntas clave.
- Asesoría personal vía Whatsapp en caso de dudas.


