Propiedades y operaciones de los números reales

Tema especial para el examen de la Universidad de Guadalajara (UdeG) 2025

¿Qué son los números reales?

Los números reales son todos aquellos números que se pueden representar en la recta numérica, es decir, que pueden ser representados con números enteros o con decimales.

Por ejemplo:

1,901,546
1
45
1.98
0.834
0.00002342343223

Este conjunto enorme de números reales se puede dividir en otros subconjuntos.

Recuerda que un subconjunto es un grupo de elementos de un conjunto total.

Por ejemplo:

El conjunto de números (-1, 0, 1 y 2)
Podemos hacer un subconjunto de este con los números (1 y 2)

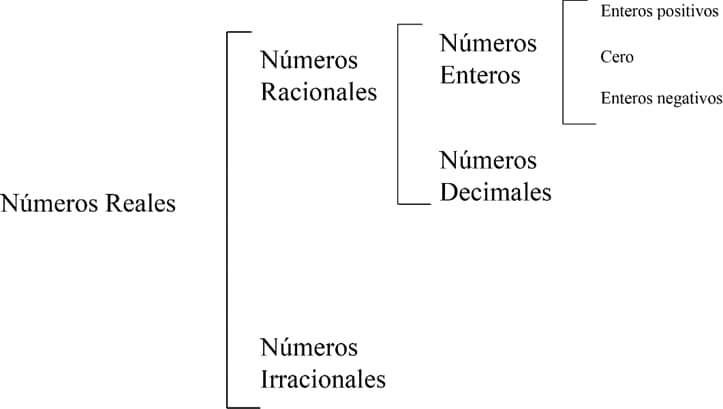
Clasificación de los números reales

Los números reales se clasifican de la siguiente forma:

Propiedades de los números reales

Las propiedades nos permiten operar con ellos de forma coherente.

Cerradura:

a y b son números reales →

a + b es un número real
a * b es un número real

Conmutativa

a + b = b + a
a * b = b * a

Asociativa:

a + (b + c) = (a + b) + c
a * (b * c) = (a * b) * c

Distributiva:

a (b + c) = ab + ac

Neutro:

a + 0 = a
a * 1 = a

Inverso:

a (-a) = 0
a * (1/a) = 1

Propiedades de orden de los números reales

1.-Tricotomía: Si a y b son reales, al compararlos solo puede ocurrir alguna de estas 3 relaciones:

a < b, b > a o a = b

2.-Transitividad: Establece la comparación entre 3 números reales:

Si a > b y b > c entonces a > c

3.-Aditividad: Dados 3 números reales (a, b y c):

Si a > b entonces a + c > b + c

4.-Multiplicativo: Dados 3 números reales (a, b y c):

Si a > b entonces a * c > b * c

Leyes de los signos

La multiplicación y la división con números enteros se basa en las leyes de los signos.

-Signos iguales el resultado es positivo
-Signos diferentes el resultado es negativo

Las operaciones básicas de los números enteros

Las operaciones básicas con números enteros son:

Adición o suma
Sustracción o resta
Multiplicaciones o Producto
División o Cociente

Suma y resta de números enteros

La suma y resta de numero enteros es la suma y resta común y corriente que todos usamos desde la primaria.

Es decir:

Si tienen diferente signo se restan
Si tienen el mismo signo se suman
y el resultado conserva el signo del número mayor en valor absoluto.

Ejemplos:

5 + 3 = 8
5 – 3 = 2
5 – 8 = -3
-2 + -4 = -6

OJO:

Si un numero entero NO tiene signo, se da por entendido que es positivo. Es decir: 5 = +5, 1 = +1, etc.

Para sumar y restar números enteros realizamos los siguiente:

Si son números con el mismo signo, sumamos los números y el resultado tendrá el mismo signo.

Ejemplos:

4 + 2 = 6
-3 + (-2) = -5
-3 – 2 = -5

Muy importante:

Recuerda que cuando un número no tiene signo, significa que es positivo; es decir, 5 = +5.

Multiplicación y división de números enteros

Para multiplicar y dividir números enteros se siguen los siguientes pasos:

Se multiplican o se dividen los números.
El resultado tendrá el signo dependiendo de las leyes de los signos:

Las leyes de los signos:

Si se multiplican o se dividen signos iguales el signo resultante es positivo.
Si se multiplican o se dividen signos diferentes el signo resultante es negativo.

Ejemplos:

(5) * (6) = 30
(-5) * (6) = -30
(-5) * (-6) = 30
(+5) * (-6) = -30
(9) ÷ (3) = 3
(9) ÷ (-3) = -3
(-9) ÷ (-3) = 3
(-9) ÷ (+3) = -3

Ojo:

Recuerda que si un número no tiene ningún signo se considera positivo: Es decir: 5 = +5

Operaciones básicas con números fraccionarios

Las operaciones con números fraccionarios y decimales son:

Suma y resta de fracciones con el mismo denominador
Suma y resta de fracciones con diferente denominador
Multiplicación (producto) de fracciones
División de fracciones

Suma y resta de fracciones con el mismo denominador

En la suma y resta de fracciones con el mismo denominador solamente se suma o se restan los numeradores, y el denominador es el mismo.

Ejemplos:

Suma y resta de fracciones con diferente denominador

En la suma y resta de fracciones con el diferente denominador primero se tienen que convertir todas las fracciones en fracciones equivalentes con el mismo denominador y así realizar una suma o resta del mismo denominador.

La otra forma para resolver suma y resta de fracciones con diferentes denominadores es obtener el mínimo común múltiplo de los denominadores dividirlo entre el denominador y multiplicarlo por el denominador de cada fracción.

PROCEDIMIENTO PARA SUMAR O RESTAR NÚMEROS DECIMALES CON DIFERENTE DENOMINADOR

1.-Se obtiene el mcm
2.-Se divide el mcm entre el denominador de cada fracción y se multiplica por su numerador, el resultado forma parte de la operación en el numerador
3.-El denominador del resultado será el mcm de los miembros de la operación

Ejemplos:

OTRA FORMA DE SUMAR Y RESTAR FRACCIONES CON DIFERENTE DENOMINADOR

IMPORTANTE

El objetivo de encontrar el mcm, es tener un denominador común para hacer una operación sencilla de suma o resta de fracciones con el mismo denominador.

Si quieres evitar el uso de mcm, puedes:

Multiplicar cada fracción (su denominar y su numerador) por un numero natural, hasta encontrar un denominar común entra las fracciones.

O multiplicar todos los denominadores y usar ese resultado como si fuera el mcm. En realidad, no es el mcm, pero los múltiplos comunes también funcionan para hacer las operaciones.

Ejemplo:

Ojo: En algunos casos esta forma te puede llevar más tiempo, pero funciona si se te olvida como obtener el mcm.

Recuerda que, si una fracción se le multiplica su numerador y su denominar por el mismo número, sigue siendo el mismo número, solo que, expresado con diferentes fracciones, (son fracciones equivalentes)

Es decir, 2/ 2 = 4/4 = 8/8, son igual a 1.

Multiplicación (producto) de fracciones

Para multiplicar fracciones con el mismo o con diferentes denominadores, simplemente se multiplican los denominadores para obtener el denominador del resultado y se multiplican los numeradores para obtener el numerador del resultado.

Ejemplos:

Resolver la multiplicación de fracciones siguiente:

Realizamos las operaciones y obtenemos:

División de fracciones

Para dividir fracciones con el mismo o con diferentes denominadores, se realiza un tipo de multiplicación cruzada. El numerador de la primera fracción se multiplica por el denominador de la segunda fracción y obtenemos el numerador del resultado, después se multiplica el denominador de la primera fracción por el numerador de la segunda fracción y obtenemos el denominador del resultado.