Tema especifico para el examen de admisión del Instituto Politécnico Nacional (IPN) 2025
¿Qué es el conteo?
El conteo en probabilidad es el proceso mediante el cual se calcula el número total de eventos o de resultados que pueden ocurrir en un fenómeno.
Es decir, en los fenómenos que ya hemos analizados, podemos decir que:
- El conteo en un volado es el número de resultados posibles, que es igual a 2. Cara o cruz
- El conteo del lanzamiento de un dado es igual a 6, porque hay 6 resultados posibles (1, 2, 3, 4, 5 y 6)
Sin embargo, existen fenómenos que es muy complicado saber el número total de posibles resultados.
Por ejemplo:
En una caja tienes 3 pelotas de color azul, roja y verde. ¿Qué probabilidades tienes de sacar primero una roja, después una verde y al último una azul?
Para poder aplicar nuestra formula que ya estudiamos:

Necesitamos saber el número total de resultados:
Para obtenerlos de manera individual, enumerados todos los posibles resultados:
- Azul, roja y verde
- Azul, verde y roja
- Roja, verde y azul
- Roja, azul y verde
- Verde, roja y azul
- Verde, azul y roja
Como veras tenemos 6 posibles resultados con solo 3 pelotas de diferentes colores. Si la cantidad de pelotas aumentará a 5, tendríamos 20 posibles resultados.
Utilidad del conteo
El conteo nos ayuda a calcular el número total de posibles resultados en un experimento.
Técnicas del conteo
Existen diferentes técnicas para poder realizar el conteo de un experimento. Las más importantes son:
- Conteo simple
- Diagramas:
- El diagrama de árbol
- Otros diagramas
- El principio multiplicativo (Principio Fundamental del Conteo (Regla del producto))
- El principio aditivo
- Permutaciones
- Combinaciones
Técnicas de conteo (probabilidad)
Existen diferentes técnicas para poder realizar el conteo de un experimento. Las más importantes son:
- Conteo simple
- Diagramas:
- El diagrama de árbol
- Otros diagramas
- El principio multiplicativo (Principio Fundamental del Conteo (Regla del producto))
- El principio aditivo
- Permutaciones
- Combinaciones
Conteo simple
Cuando son pocos el numero total de resultados de un experimento, los podemos contar simplemente, como ya lo hicimos en el caso del dado o del volado.
En el caso del dado, tenemos un total de 6 posibles resultados (1, 2, 3, 4, 5 y 6)
Y en el caso de la moneda solo (cara o cruz) o sea 2 posibles resultados.
Diagramas:
Cuando son un poco mas posibles resultados, pero no tantos, podemos usar diagramas para enumerarlos.
Por ejemplo, cuando se lanzan 2 dados y queremos saber el numero total de resultados posibles.
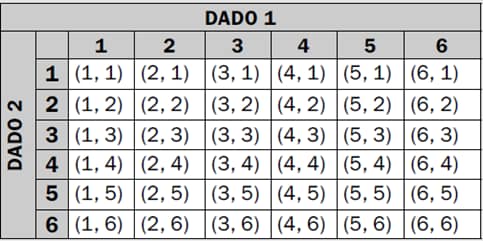
Con esto podemos ver que tenemos 36 posibles resultados. Y si queremos saber que probabilidad tenemos de obtener un 6 con los 2 dados. Tenemos que saber el numero total de casos favorables al 6.
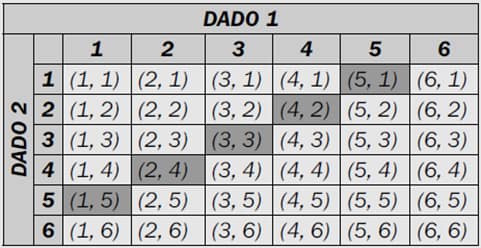
Por lo que la probabilidad de que obtengamos un 6 de los 2 dados es:
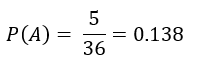
O 13.8%
El diagrama de árbol
El diagrama de árbol consiste en representar todos los eventos posibles de un experimento a través de líneas rectas convergentes.
Ejemplo 1:
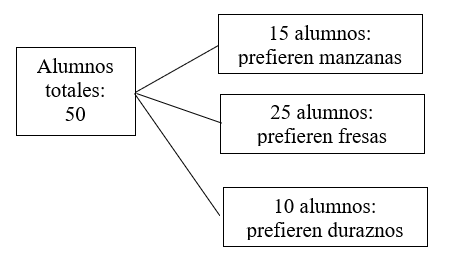
En un salón de clases, 15 alumnos les gustan las manzanas, otros 25 alumnos les gustan las fresas y otros 10 alumnos les gustan los duraznos.
Si eliges a un alumno al azar de este salón de clases, ¿qué probabilidades tienes de seleccionar a un alumno que le gusten los duraznos?
La probabilidad de que un alumno prefiera duraznos es:

Es decir, tenemos 20% de probabilidades de que al seleccionar a un alumno al azar le gusten los duraznos.
Ejemplo 2:
¿Qué probabilidades tienes de obtener cara-cara en un bolado de doble lanzamiento?
Dibujamos las posibles opciones:
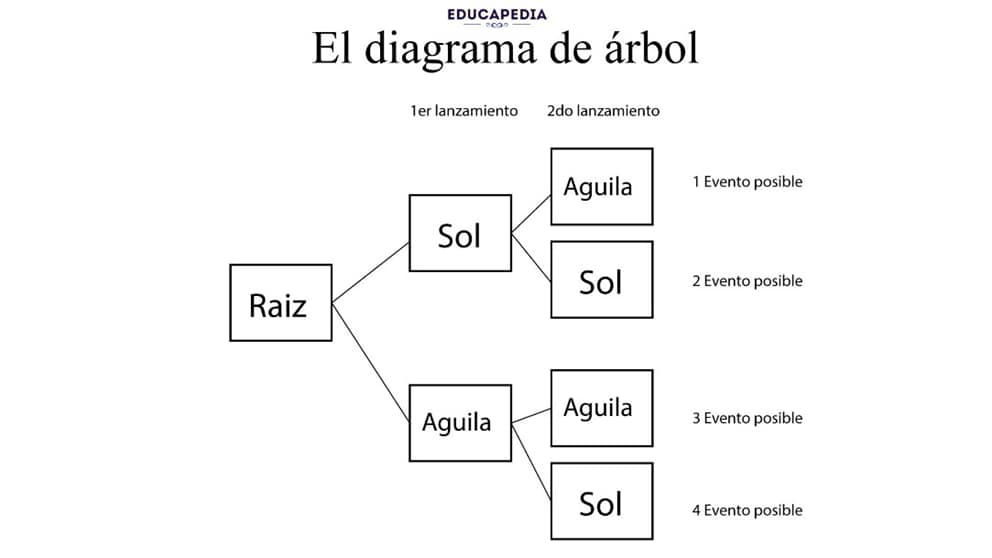
Con esto, podemos observar que el número total de eventos es igual a 4, por lo que aplicando nuestra formula tenemos:

Es decir, tenemos 25% de probabilidades de que obtengamos en el primer lanzamiento cara y en el segundo lanzamiento otra vez cara.
El principio aditivo
En un experimento compuesto por dos sucesos independientes, es decir, que ocurren de manera separa uno del otro, la cantidad total de posibles resultados es igual a la suma de los posibles resultados de un suceso más los posibles resultados del 2do suceso.
# total de eventos = # de posibles resultados del 1er suceso + # de posibles resultados del 2do suceso
Ejemplo:
Para conocer el número total de eventos en un juego de lanzamiento de dos dados, uno independiente del otro, tenemos que:
# total de eventos = # de posibles resultados del 1er suceso + # de posibles resultados del 2do suceso
# total de eventos = 6 + 6 = 12
Si quisiéramos conocer cuál es la probabilidad de obtener un 5 o un 4 en alguna de las tiradas de los dados:
Tendríamos:
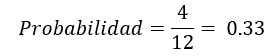
Y podríamos decir que tenemos el 33% de probabilidades de obtener un 4 o un 5 en alguna de las tiradas de los dados.
El principio multiplicativo
En un experimento compuesto por 2 sucesos interdependientes, cada uno con un posible resultado, para calcular el número total de posibles resultados compuestos es igual a la multiplicación de los posibles resultados del primer suceso por los posibles resultados del segundo suceso.
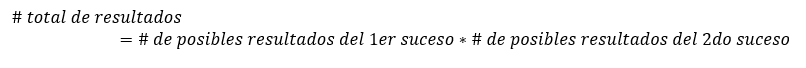
Ejemplo:
En el lanzamiento de dos dados, queremos saber que probabilidad tenemos de obtener un 6. Para calcular la probabilidad ocupamos nuestra formula, pero como no sabemos el número total de posibles resultados, podemos hacer una diagrama de árbol o aplicar el principio multiplicativo.
Por lo cual tendríamos:

Lo que nos indica que tenemos 36 posibles resultados.
Para obtener un 6, podemos construirlo con: 4+2, 2+4, 5+1, 1+5, 3+3, 3+3.
Aplicando nuestra fórmula para obtener la probabilidad obtenemos:

Lo que podemos decir es que tenemos 16% de probabilidades de obtener un 6 en nuestra tirada de dos dados.
Combinaciones
Una combinación es un subconjunto de elementos de un conjunto mayor, donde no importa el orden de estos elementos.
Para calcular el número de combinaciones posibles en un conjunto de elementos aplicamos la formula:
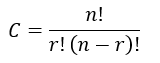
Donde:
n = tamaño del conjunto
r = tamaño de la combinación
x! (se lee equis factorial) = x * (x-1) * (x-2)… (n – n-1)
Ejemplo 1:
Tenemos 3 pelotas color azul, rojo y verde, ¿Cuantas combinaciones podemos formar de 2 pelotas?
Como no importa el orden, podemos formar las siguientes posibilidades:
- Azul y rojo
- Azul y verde
- Rojo y verde
Es decir, solo 3 combinaciones de 2 pelotas podemos formar con 3 pelotas diferentes.
Aplicando la formula obtenemos:
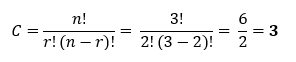
Ejemplo 2:
Si en nuestro salón de clases hay 30 alumnos, ¿cuántas combinaciones de 5 elementos podemos formar?
Posiblemente estas pensado que podemos formar 6 grupos de 5 elementos, pero esto es incorrecto, porque cuando se forman estos grupos, “solo es 1 posibilidad de formar los 5 grupos”.
Aplicando nuestra formula obtenemos:
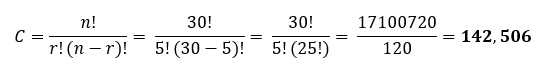
Es decir, tenemos 142,506 posibles combinaciones de 5 personas en un salón de 30.
Permutaciones
Una permutación es un grupo de elementos igual o de menor tamaño que del conjunto mayor, donde sí importa el orden de estos elementos.
Existen 3 tipos de permutaciones:
- Permutaciones sin repetición
- Permutaciones con repetición
- Permutaciones con n elementos tomados de r en r.
Permutaciones sin repetición
De n elementos distintos, tomados todos, hay:
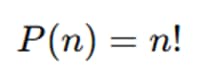
Ejemplo:
¿Cuántas formas hay de ordenar las letras A, B y C?
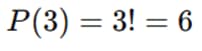
(Las ordenaciones son: ABC, ACB, BAC, BCA, CAB, CBA).
Permutaciones con repetición
Si algunos elementos se repiten, la fórmula es:
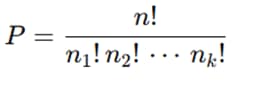
Ejemplo:
¿Cuántas formas distintas hay de ordenar las letras de la palabra “MAMA”?
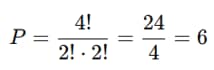
Permutaciones con n elementos tomados de r en r
Si se seleccionan r elementos de n y se ordenan:
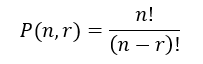
Donde:
n = tamaño del conjunto
r = tamaño de la permutación
x! (se lee equis factorial) = x * (x-1) * (x-2)… (n – n-1)
Ejemplo 1:
En el mismo problema de las 3 pelotas color azul, rojo y verde, ¿Cuántas permutaciones podemos formar de 2 pelotas?
Como si importa el orden, podemos formar las siguientes posibilidades:
- Azul y rojo
- Rojo y azul
- Azul y verde
- Verde y azul
- Rojo y verde
- Verde y rojo
Es decir, 6 permutaciones de 2 pelotas podemos formar con 3 pelotas diferentes.
Aplicando la formula obtenemos:
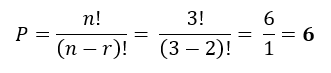
Ojo:
Como ahora si consideramos el orden de las pelotas, podemos hacer más subgrupos (permutaciones) que combinaciones.
Ejemplo 2:
Si en nuestro salón de clases hay 30 alumnos, ¿cuántos permutaciones de 5 elementos podemos formar?
Aplicando nuestra formula obtenemos:

Es decir, tenemos 17,100,720 posibles permutaciones de 5 personas en un salón de 30.
Próximo tema como lo marca la guía oficial para el examen del IPN 2025:
También esta disponible la guía de matemáticas para el examen del IPN 2025
Guia desarrollada de Matematicas para el examen del IPN
Prepárate de forma clara y organizada para tu examen al Instituto Politécnico Nacional 2025
Esta guía incluye explicaciones sencillas, ejemplos prácticos y ejercicios resueltos de los temas clave de matemáticas que suelen aparecer en el examen.
Diseñada para estudiantes de preparatoria, te ayudará a reforzar conocimientos, ahorrar tiempo de estudio y aumentar tu confianza el día de la prueba.


